Chapter 12 - Queues and Deques

In Erlang you have noticed that it is more efficient to access the front of a list as opposed to the back of the list. This means that it is very efficient to implement a stack. Queues on the other hand are more expensive since we have to recursively traverse to the end of the list to enqueue new values. To resolve this problem we will use a technique that combines two stacks together to form a queue.

12.1 Queues

The basic functions of a queue include the ability to do the following:

• enqueue - insert a new value at the back (or end) of the queue
• dequeue - remove a value from the front (or start) of the queue
• head - get the value from the front of the queue

If we used a list to do this, we would have O(1) for the dequeue and the head but O(n) for the enqueue. To resolve this problem, we will use two lists and treat both them as stacks as follows:

• Front - This stack will always have the next value to dequeue available at the front of the stack. The head function will use this stack as well.
  
• Back - This stack will always have the most recent value enqueued be available at the front of the stack.

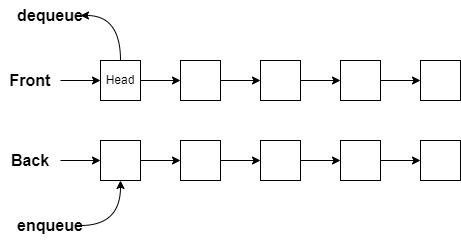
The dilemma with this arrangement is that we have no way to get values added to Back to migrate over to the Front. This would mean that Front would always be empty. To resolve this problem we introduce a rule, or an invariant, which is that the Front can only be empty if the Back is also empty. If both are empty, then we say the queue is empty as well. This rule requires us to move items between the two stacks as needed.

We will store both stacks in a single structure:

\(struct ~ ~ queue \lbrace [a] : Front, [a] : Back \rbrace.\)

\(\nonumber\)

Our three functions are specified as follows:

\(spec ~ ~ enqueue :: a ~ ~ queue \rightarrow queue.\)

\(spec ~ ~ dequeue :: queue \rightarrow queue.\)

\(spec ~ ~ head :: queue \rightarrow a.\)

\(\nonumber\)

When calling the enqueue function, we must ensure that Front is only empty when Back is empty. Normally, we put the new value into the Back stack. However, if both stacks are empty, then we will put the first new value into the Front.

Operation	Front	Back
Create Empty	[]	[]
Enqueue 1	[1]	[]
Enqueue 2	[1]	[2]
Enqueue 3	[1]	[3,2]
Enqueue 4	[1]	[4,3,2]

The definition for this behavior is shown below:

\(de\mathit{f} ~ ~ enqueue :: Value ~ ~ \lbrace [], [] \rbrace \rightarrow \lbrace [Value], [] \rbrace;\)

\(de\mathit{f} ~ ~ enqueue :: Value ~ ~ \lbrace Front, Back \rbrace \rightarrow \lbrace Front, [Value|Back] \rbrace.\)

\(\nonumber\)

Ensuring our rule regarding the Front being empty only when Back is empty is a little more complicated for the dequeue function. Normally we remove the value from the Front stack. However, if the Front stack only has one value, then we must prevent it from going empty. This is accomplished by taking the values in the Back and moving them to the Front. However, the order of the values must be swapped because the first one of the Back should be the last one to be removed from the Front.

Operation	Front	Back
Queue from Previous Table	[1]	[4,3,2]
Dequeue 1	[2,3,4]	[]
Dequeue 2	[3,4]	[]
Enqueue 5	[3,4]	[5]
Enqueue 6	[3,4]	[6,5]
Dequeue 3	[4]	[6,5]
Dequeue 4	[5,6]	[]

Note in the definition below the first clause is for error checking (can’t dequeue from an empty queue). Also, we assume a reverse function is available:

\(de\mathit{f} ~ ~ dequeue :: \lbrace [], [] \rbrace \rightarrow \lbrace [], [] \rbrace;\)

\(de\mathit{f} ~ ~ dequeue :: \lbrace [One], Back \rbrace \rightarrow \lbrace (reverse ~ ~ Back), [] \rbrace;\)

\(de\mathit{f} ~ ~ dequeue :: \lbrace [First|Rest], Back \rbrace \rightarrow \lbrace Rest, Back \rbrace.\)

\(\nonumber\)

Our head function is really simple since we ensured that the Front would never be empty when the queue was empty.

\(de\mathit{f} ~ ~ head :: \lbrace [], [] \rbrace \rightarrow nil;\)

\(de\mathit{f} ~ ~ head :: \lbrace [First|Rest], Back \rbrace \rightarrow First.\)

\(\nonumber\)

Problem Set 1

Starting Code: prove12_1/src/prove12_1.erl

1. Implement the enqueue, dequeue, and head functions as described in the definitions above. Use the test code provided to verify your implementations. A create and empty function are already provided for you. In the test code, the check_queue will verify that the queue was created correctly.

12.2 Deques

Common queue implementations also include double-ended support. Called a deque (pronounced ‘deck’), this should include support for the following additional functions:

• enqueue_front - insert a new value at the front of the queue
• dequeue_back - remove a value from the back of the queue
• tail - get the value from the back of the queue

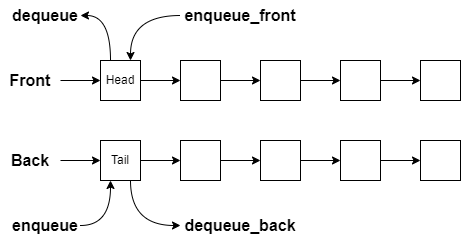
The rule that we had for the Queue (Front can’t be empty unless the Back was empty also) resulted in us having a simple head function. If we don’t do something similar for our new deque functions, we will be forced to use recursion for our Tail. Right now it is very common for our Front to contain all the values because we reversed the values from Back and moved them all over. This would mean that we would need to recurse to the end of Front to find the tail.

We introduce an modified rule for the Deque which is that neither the Front nor the Back can be empty if there are 2 or more items in the Deque. This means that our stacks will always take the following formats:

• Front is empty and Back is empty - Empty Deque
• Front has one item and Back is empty - Deque with only one item
• Front is empty and Back has one item - Another valid deque with only one item
• Front is not empty and Back is not empty - Deque with more than two or more items

For this to work, we will need to modify our approach for dequeue that said to reverse all the values from Back and move them to the Front. This action would cause Front to have potentially more than one item and Back to be empty.

Instead of reversing and moving all of the Back on a dequeue, we will reverse and move only half of the values. This will ensure that we will always still have some value in the Back (assuming we have 2 or more items still in the deque).

Operation	Front	Back
Queue from Previous Table	[1]	[4,3,2]
Dequeue 1	[2,3]	[4]
Dequeue 2	[3]	[4]
Enqueue 5	[3]	[5,4]
Enqueue 6	[3]	[6,5,4]
Enqueue 7	[3]	[7,6,5,4]
Dequeue 3	[4,5]	[7,6]
Dequeue 4	[5]	[7,6]
Dequeue 5	[6]	[7]
Dequeue 6	[7]	[]

With the definition below, we will assume we have a split and a length function that we will use to split a list into two halves.

\(de\mathit{f} ~ ~ dequeue :: \lbrace [One], Back \rbrace \rightarrow\)

\(\quad \quad \lbrace List1, List2 \rbrace = (split ~ ~ (length ~ ~ Back) / 2 ~ ~ Back),\)

\(\quad \quad \lbrace (reverse ~ ~ List2), List1 \rbrace;\)

\(\nonumber\)

Since it is possible with our new rule that the Back may have the one item instead of the Front, we also need a new clause for this situation:

\(de\mathit{f} ~ ~ dequeue :: \lbrace [], [One] \rbrace \rightarrow \lbrace [], [] \rbrace;\)

\(\nonumber\)

A similar consideration needs to be made with our head function by adding this new clause:

\(de\mathit{f} ~ ~ head :: \lbrace [], [One] \rbrace \rightarrow One;\)

\(\nonumber\)

To implement our three new functions, we will make them symmetrical with the three we already have. The enqueue_front function will put the first new value in the Back and subsequent values in the Front. There is another special case we need to consider. What if the first call was to enqueue and then enqueue_front was called. The enqueue function would put the first value in the Front. If enqueue_front was called second, it would put the “subsequent” values in the Front as well thus causing an imbalance which is against our rules. Therefore, we have included the 2nd clause to put the previous value added into the Back and the new value added into the Front.

\(de\mathit{f} ~ ~ enqueue\_front :: Value ~ ~ \lbrace [], [] \rbrace \rightarrow \lbrace [], [Value] \rbrace;\)

\(de\mathit{f} ~ ~ enqueue\_front :: Value ~ ~ \lbrace [One], [] \rbrace \rightarrow \lbrace [Value], [One] \rbrace;\)

\(de\mathit{f} ~ ~ enqueue\_front :: Value ~ ~ \lbrace Front, Back \rbrace \rightarrow \lbrace [Value|Front], Back \rbrace.\)

\(\nonumber\)

That special case we added to enqueue_front also needs to be provided for in the enqueue function. The 2nd clause below is added new for our deque. In this case, we have to swap the first value to be in the Front allowing the second value to be put in the Back.

\(de\mathit{f} ~ ~ enqueue :: Value ~ ~ \lbrace [], [] \rbrace \rightarrow \lbrace [Value], [] \rbrace;\)

\(de\mathit{f} ~ ~ enqueue :: Value ~ ~ \lbrace [], [One] \rbrace \rightarrow \lbrace [One], [Value] \rbrace;\)

\(de\mathit{f} ~ ~ enqueue :: Value ~ ~ \lbrace Front, Back \rbrace \rightarrow \lbrace Front, [Value|Back] \rbrace.\)

\(\nonumber\)

The dequeue_back function will check for a single item in the Front, check for a potential empty list in the Back requiring a transfer of half the values in the Front to move to the Back, or a normal removal of the first value in the Back.

\(de\mathit{f} ~ ~ dequeue\_back :: \lbrace [], [] \rbrace \rightarrow \lbrace [], [] \rbrace;\)

\(de\mathit{f} ~ ~ dequeue\_back :: \lbrace [One], [] \rbrace \rightarrow \lbrace [], [] \rbrace;\)

\(de\mathit{f} ~ ~ dequeue\_back :: \lbrace Front, [One] \rbrace \rightarrow\)

\(\quad \quad \lbrace List1, List2 \rbrace = (split ~ ~ (length ~ ~ Front) / 2 ~ ~ Front),\)

\(\quad \quad \lbrace List1, (reverse ~ ~ List2) \rbrace;\)

\(de\mathit{f} ~ ~ dequeue\_back :: \lbrace Front, [First|Rest] \rbrace \rightarrow \lbrace Front, Rest \rbrace.\)

\(\nonumber\)

The tail function will check for either a single value in the Front or the first value in the Back.

\(de\mathit{f} ~ ~ tail :: \lbrace [], [] \rbrace \rightarrow nil;\)

\(de\mathit{f} ~ ~ tail :: \lbrace [One], [] \rbrace \rightarrow One;\)

\(de\mathit{f} ~ ~ tail :: \lbrace Front, [First|Rest] \rbrace \rightarrow First.\)

\(\nonumber\)

Problem Set 2

Starting Code: prove12_2/src/prove12_2.erl

1. Implement the enqueue_front, dequeue_back, and tail functions as described in the definitions above. You will also need to modify the dequeue and head to support the deque. Use the test code provided to verify your implementations. You will need to use the lists:split function provided in Erlang.

\(\nonumber\) \(\nonumber\)