Chapter 5 - Higher Order Functions - Fold and Unfold

The fold and unfold are also common higher order functions. A fold will convert from a list to a single value whereas an unfold will convert from a single value to a list.

5.1 Fold

Just like the map and filter patterns, we will use a lambda function to define what we want to do with each item of the list. Unlike the map and filter, we will not apply the lambda function to determine what to put in the resulting list. Instead (in the case of fold) we will use the lambda function to determine how each item in our list contributes to the one single value result. The lambda function is used to combine all the values in the list.

If I have a list of numbers [1 2 3 4 5] that I wanted to add, then a lambda function would take each number (\(Value\)) and add it to an accumulator (\(Acc\)):

\(spec ~ ~ \lambda :: real ~ ~ real \rightarrow real.\)

\(de\mathit{f} ~ ~ \lambda :: Value ~ ~ Acc \rightarrow Acc + Value.\)

\(\nonumber\)

If I wanted to add the squares of the numbers in the list, then I would want the lambda function to be

\(spec ~ ~ \lambda :: real ~ ~ real \rightarrow real.\)

\(de\mathit{f} ~ ~ \lambda :: Value ~ ~ Acc \rightarrow Acc + (Value * Value).\)

\(\nonumber\)

The result of the lambda functions will be passed in as the accumulator value when we goto the next item in the list. This implies that we will need to define what the initial accumulator value should be.

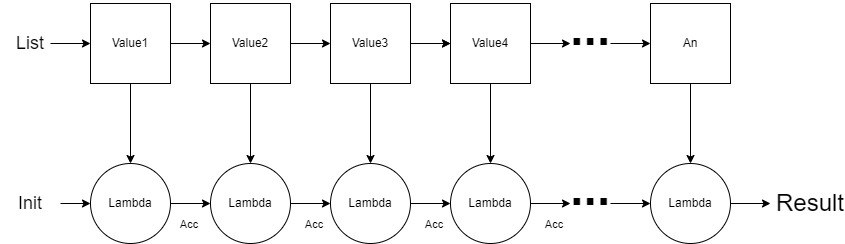
Notice that the fold function is expecting that the lambda to always have 2 input parameters where the second parameter is the accumulator. The single output of the \(\lambda\) function is the updated accumulator.

Here is the formal definition of the fold:

\(spec ~ ~ \lambda :: a_1 ~ ~ a_2 \rightarrow a_2.\)

\(spec ~ ~ \mathit{fold} :: \lambda ~ ~ a_2 ~ ~ [a_1]\rightarrow a_2.\)

\(de\mathit{f} ~ ~ \mathit{fold} :: \lambda ~ ~ Acc ~ ~ []\rightarrow Acc;\)

\(de\mathit{f} ~ ~ \mathit{fold} :: \lambda ~ ~ Acc ~ ~ [First|Rest] \rightarrow (\mathit{fold} ~ ~ \lambda ~ ~ (\lambda ~ ~ First ~ ~ Acc) ~ ~ Rest).\)

\(\nonumber\)

Notice the recursive nature of the fold as it applies the lambda function to the each element one at a time starting with the first element (\(First\)). The result of calling the lambda function (\(\lambda ~ ~ First ~ ~ Acc\)) becomes the new accumulator value when fold is called recursively on the remainder of the list (\(Rest\)).

Consider the code implementation below.

fold(_Lambda, Acc, []) -> Acc;
fold(Lambda, Acc, [First|Rest]) -> fold(Lambda, Lambda(First, Acc), Rest).

The initial Acc passed to the fold function represents the initial value of the accumulator. If we were summing up numbers in a list, we would expect the initial accumulator to be 0.

Note that Erlang provides this function as a built-in function called lists:foldl (meaning fold left).

Problem Set 1

Starting Code: prove05_1/src/prove05_1.erl

Implement the the fold function.
Modify fold_2_test by creating a lambda function to use with your fold function to concatenate a list of strings. Note that you can use the ++ operator to solve this problem. Test code is provided for you in the starting code.
Modify fold_3_test by creating a lambda function to use with your fold function to count the number of items in a list. Test code is provided for you in the starting code.
Modify fold_4_test by creating a lambda function to use with your fold function to reverse a list. Note that the single result that a fold returns can be a list if the lambda function is written properly. Test code is provided for you in the starting code.

5.2 Fold Right

When you look at the definition of fold notice that the list is processed from left to right. We can define a function that goes from right to left called foldr. This function will require us to traverse to the end of the list before we can actually call the lambda function. In some cases, folding right instead of folding left will result in different results.

\(spec ~ ~ \lambda :: a_1 ~ ~ a_2 \rightarrow a_2.\)

\(spec ~ ~ \mathit{foldr} :: \lambda ~ ~ a_2 ~ ~ [a_1]\rightarrow a_2.\)

\(de\mathit{f} ~ ~ \mathit{foldr} :: \lambda ~ ~ Acc ~ ~ [] \rightarrow Acc;\)

\(de\mathit{f} ~ ~ \mathit{foldr} :: \lambda ~ ~ Acc ~ ~ [First|Rest]\rightarrow (\lambda ~ ~ First ~ ~ (\mathit{foldr} ~ ~ \lambda ~ ~ Acc ~ ~ Rest)).\)

\(\nonumber\)

The code implementation of our function in Erlang is left for an exercise below. Erlang provides a built-in function called lists:foldr to perform this task.

Problem Set 2

Starting Code: prove05_2/src/prove05_2.erl

Implement foldr and modify foldr_test with the same concatenation lambda you used in the previous problem set (see fold_2_test). Observe the different behavior with the right fold versus the left fold done previously.

5.3 Unfold

The fold design pattern is used when you want to consolidate from one larger thing to a smaller thing such as a list to a single value. If we want to go backwards, this is called an unfold. Note that folding and unfolding are not inversely related. For example, if I had a list of numbers [2 5 3 1] and I folded them up using a simple sum function, I would get 11. However, if started with 11 and worked backwards, I could get a possible solution such as [7 1 3 0] which is different from our original list.

When we unfold, we are relying on some initial conditions to generate the next value for our list.

Suppose we wanted to generate a list repeated numbers. The number to repeat we will call \(Value\) and the number of repeated values we will call \(Count\). We want to unfold our initial conditions (\(Value\) and \(Count\)) to obtain the list of numbers. For example, if \(Count\) is 4 and \(Value\) is 6, then the gensame function should result in [6 6 6 6]. Here is a definition for our gensame function:

\(spec ~ ~ gensame :: integer ~ ~ real \rightarrow [real].\)

\(de\mathit{f} ~ ~ gensame :: 0 ~ ~ Value \rightarrow [];\)

\(de\mathit{f} ~ ~ gensame :: Count ~ ~ Value \rightarrow [Value | (gensame ~ ~ (Count-1) ~ ~ Value)].\)

\(\nonumber\)

Here is the Erlang code for gensame:

gensame(0, _Value) -> [];
gensame(Count, Value) -> [Value | gensame(Count-1, Value)].

We could modify this function to create an increasing sequence of numbers by including an initial value (\(Init\)) and step size (\(Step\)). To accomplish this, we need to define a lambda function to calculate the next value. We will use \(Curr\) to represent the current value that started with \(Init\) and was increased by \(Step\).

For example, if we wanted a list of 5 even numbers starting at 4, then \(Count\) would be 5, \(Init\) would be 4, and our lambda would be:

\(spec ~ ~ \lambda :: real \rightarrow real.\)

\(de\mathit{f} ~ ~ \lambda :: Curr \rightarrow Curr + 2.\)

\(\nonumber\)

The output of our genincr function would be [4 6 8 10 12].

\(spec ~ ~ genincr :: integer ~ ~ real ~ ~ \lambda \rightarrow [real].\)

\(de\mathit{f} ~ ~ genincr :: 0 ~ ~ Curr ~ ~ \lambda \rightarrow [];\)

\(de\mathit{f} ~ ~ genincr :: Count ~ ~ Curr ~ ~ \lambda \rightarrow [Curr | (genincr ~ ~ (Count-1) ~ ~ (\lambda ~ ~ Curr) ~ ~ \lambda)].\)

\(\nonumber\)

Looking at these two examples, we can generalize our function. Let’s create a generic unfold function that works for more than just numbers.

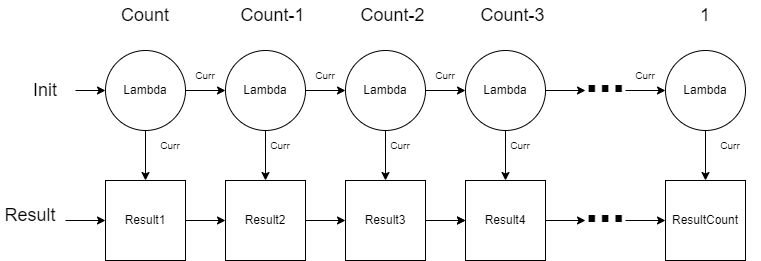
This function does not exist in the Erlang library primarily because its not generic enough. We could have other means to replace \(Count\) or we can even create a stream (we will see those later in the course). For our purposes, we will create a generic unfold function that uses \(Count\) but has a generic \(\lambda\) that works with any type. The specification and definition is give below:

\(spec ~ ~ \lambda :: a \rightarrow a.\)

\(spec ~ ~ unfold :: integer ~ ~ a ~ ~ \lambda \rightarrow [a].\)

\(de\mathit{f} ~ ~ unfold :: 0 ~ ~ Curr ~ ~ \lambda \rightarrow [];\)

\(de\mathit{f} ~ ~ unfold :: Count ~ ~ Curr ~ ~ \lambda \rightarrow [Curr | (unfold ~ ~ (Count-1) ~ ~ (\lambda ~ ~ Curr) ~ ~ \lambda)].\)

\(\nonumber\)

The Erlang code for unfold is given below:

unfold(0, _Curr, _Lambda) -> [];
unfold(Count, Curr, Lambda) -> [Curr|unfold(Count-1, Lambda(Curr), Lambda)].

Problem Set 3

Starting Code: prove05_3/src/prove05_3.erl

Implement the unfold function.
Use the unfold function to modify unfold_2_test to generate a geometric sequence of six numbers starting at 1 with a factor of \(1/2\) ([1, 0.5, 0.25, 0.125, 0.0625, 0.03125]).
Write a function called range that takes in \(Start\), \(Size\), and \(Step\) parameters (in that order) and returns a list of length \(Size\) starting at \(Start\), stepping by \(Step\). Your range function must use the unfold function. For example, range(3,5,4) would return [3, 7, 11, 15, 19]. You should assume that both \(Size\) and \(Step\) are positive integers greater than 0.

\(\nonumber\) \(\nonumber\)